本答案将介绍js中常用的几种排序算法，并结合v8中相关源码分析sort实现的策略

常见排序算法

首先温习下排序算法需要关注的两大要素

时间复杂度

描述该算法的运行时间，通常用大O描述，附上一张时间复杂度曲线图帮助理解

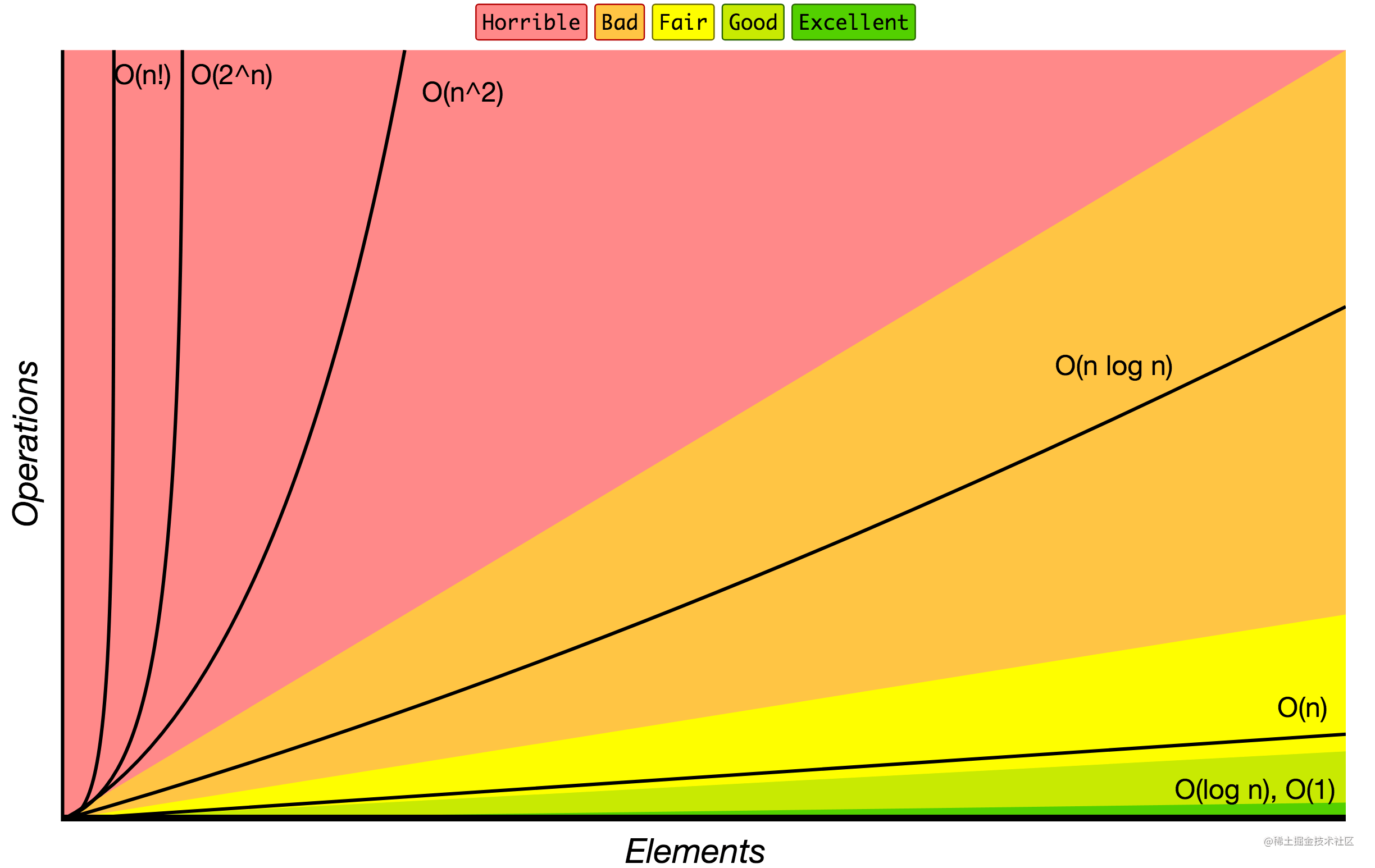
空间复杂度

度量一个算法在运行过程中占用存储空间大小

常见排序

常见的十大经典排序算法就不在这科普了，根据特性可将它们从不同角度进行分类

• 是否基于比较：比较类排序和非比较类排序

• 是否稳定：稳定类排序和不稳定类排序

通常我们从是否基于排序的视角进行分类

• 比较类排序

  通过比较来决定元素间的相对次序，其时间复杂度不能突破 O(nlogn)，因此也称为非线性时间比较类排序。

• 非比较类排序

  不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

具体分类枚举可以结合下图理解

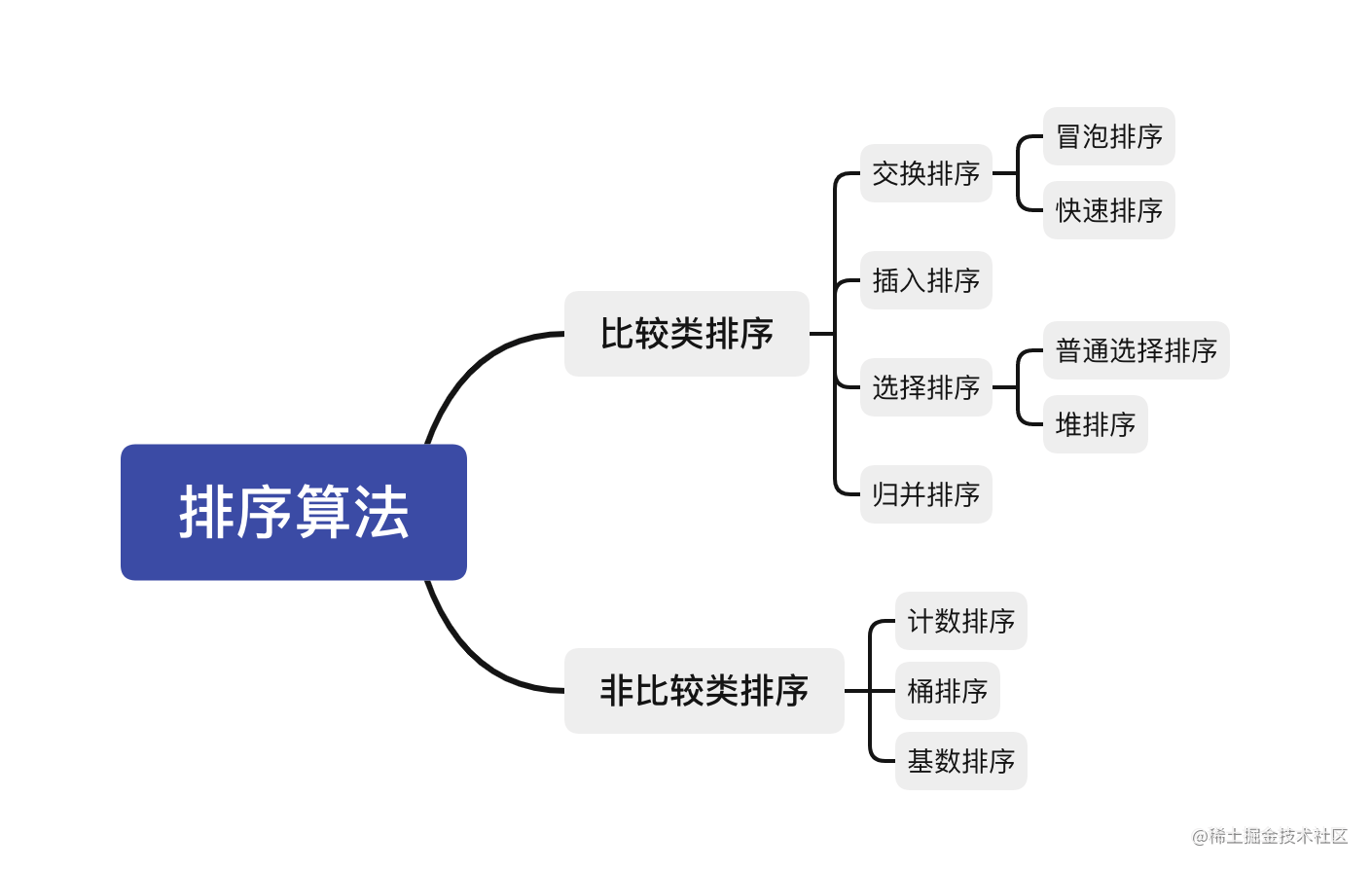
接下来我们写下几个常见的经典排序

快速排序

快速排序主要使用递归分支的思想，通过一趟排序，将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可以分别对这两部分记录继续进行排序，以达到整个序列有序。

复制
1var a = [ 25, 76, 34, 232, 6, 456, 221];
2function quickSort(array) {
3  var quick = function(arr) {
4    if (arr.length <= 1) return arr
5    const index = Math.floor(len >> 1)
6    const pivot = arr.splice(index, 1)[0]
7    const left = []
8    const right = []
9    for (let i = 0; i < arr.length; i++) {
10      if (arr[i] > pivot) {
11        right.push(arr[i])
12      } else if (arr[i] <= pivot) {
13        left.push(arr[i])
14      }
15    }
16    return quick(left).concat([pivot], quick(right))
17  }
18  const result = quick(array)
19  return result
20
21}
22quickSort(a);//  [ 6, 25, 34, 76, 221, 232, 456]

堆排序

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质，即子结点的键值或索引总是小于（或者大于）它的父节点。堆的底层实际上就是一棵完全二叉树，可以用数组实现。

根节点最大的堆叫作大根堆，根节点最小的堆叫作小根堆，你可以根据从大到小排序或者从小到大来排序，分别建立对应的堆就可以。请看下面的代码。

复制
1var a = [25, 76, 34, 232, 6, 456, 221];
2function heap_sort(arr) {
3  var len = arr.length
4  var k = 0
5  function swap(i, j) {
6    var temp = arr[i]
7    arr[i] = arr[j]
8    arr[j] = temp
9  }
10
11  function max_heapify(start, end) {
12    var dad = start
13    var son = dad * 2 + 1
14    if (son >= end) return
15    if (son + 1 < end && arr[son] < arr[son + 1]) {
16      son++
17    }
18    if (arr[dad] <= arr[son]) {
19      swap(dad, son)
20      max_heapify(son, end)
21    }
22  }
23  for (var i = Math.floor(len / 2) - 1; i >= 0; i--) {
24    max_heapify(i, len)
25  }
26
27  for (var j = len - 1; j > k; j--) {
28    swap(0, j)
29    max_heapify(0, j)
30  }
31  return arr
32}
33
34heap_sort(a); // [6, 25, 34, 76, 221, 232, 456]

归并排序

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

复制
1var a = [25, 76, 34, 232, 6, 456, 221];
2function mergeSort(array) {
3  const merge = (right, left) => {
4    const result = []
5    let il = 0
6    let ir = 0
7    while (il < left.length && ir < right.length) {
8      if (left[il] < right[ir]) {
9        result.push(left[il++])
10      } else {
11        result.push(right[ir++])
12      }
13    }
14    while (il < left.length) {
15      result.push(left[il++])
16    }
17    while (ir < right.length) {
18      result.push(right[ir++])
19    }
20    return result
21  }
22  const mergeSort = array => {
23    if (array.length === 1) { return array }
24    const mid = Math.floor(array.length / 2)
25    const left = array.slice(0, mid)
26    const right = array.slice(mid, array.length)
27    return merge(mergeSort(left), mergeSort(right))
28  }
29  return mergeSort(array)
30}
31mergeSort(a); // [6, 25, 34, 76, 221, 232, 456]
32

最后附上一张各排序算法统计对照表:

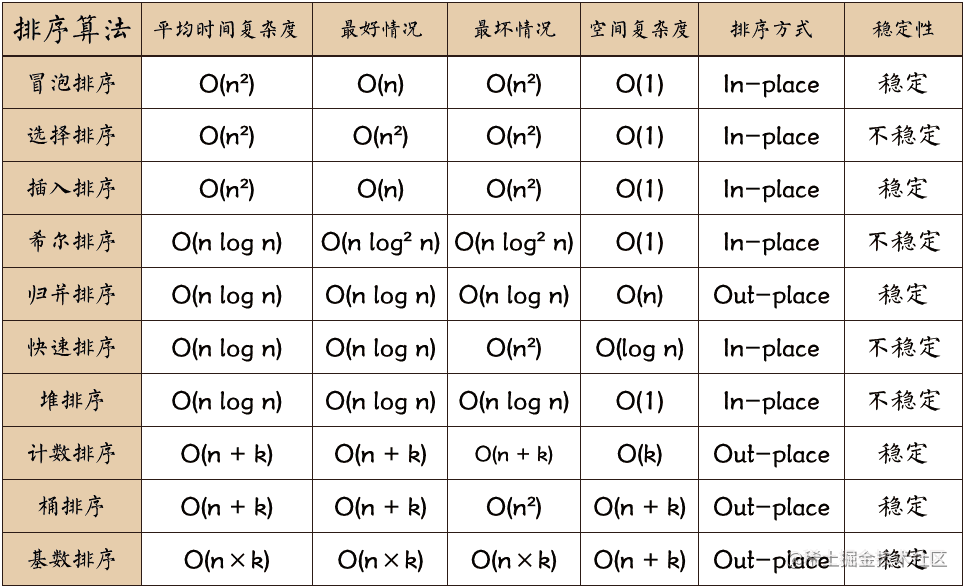
js中的sort方法

sort方法基本使用

arr.sort([compareFunction])

如果不传入 compareFunction，则元素按照转换为字符串的各个字符的 Unicode 位点进行排序，有些同学经常在整数排序上犯错误，多半是因为遗漏了这一规则

复制
1const names = ['tom', 'jesse', 'jack'];
2names.sort();
3
4console.log(names);
5// ["jack", "jesse", "tom"]
6
7const array1 = [1, 30, 4, 21, 100000];
8array1.sort();
9
10console.log(array1);
11// [1, 100000, 21, 30, 4]

如果指明了 compareFunction 参数 ，那么数组会按照调用该函数的返回值排序，即 a 和 b 是两个将要被比较的元素：

• compareFunction（a, b）< 0，a 会被排列到 b 之前
• compareFunction（a, b）=== 0，a 和 b 的相对位置不变
• compareFunction（a, b）> 0，b 会被排列到 a 之前

sort源码分析

查阅 v8源码sort部分 我们可以发现，对于需要排序的元素个数n，具体排序策略有几下中情形：

• 当 n<=10 时，采用插入排序；
• 当 n>10 时，采用三路快速排序；
• 10<n <=1000，采用中位数作为哨兵元素；
• n>1000，每隔 200~215 个元素挑出一个元素，放到一个新数组中，然后对它排序，找到中间位置的数，以此作为中位数。

乍一看结论你可能会纠结两个问题

1、为何元素较少的时候要用快排

其实仔细分析一下不难究其原因。对于插排和快排，理论上的平均时间复杂度分别为O(n^2)和O(nlogn)，其中插排在最好情况下的时间复杂度是 O(n)。对比不难得出结论，当n足够小的时候，快排优势变小。事实上插排经优化后对于小数据集的排序性能可以超过快排。

2、为何要选择哨兵元素

因为快速排序的性能瓶颈在于递归的深度，最坏的情况是每次的哨兵都是最小元素或者最大元素，那么进行 partition（一边是小于哨兵的元素，另一边是大于哨兵的元素）时，就会有一边是空的。如果这么排下去，递归的层数就达到了n, 而每一层的复杂度是 O(n)，因此快排这时候会退化成O(n^2)级别。

这种情况是要尽力避免的，那么如何来避免？就是让哨兵元素尽可能地处于数组的中间位置，让最大或者最小的情况尽可能少

最后我们看下源码中的sort的基本结构

复制
1function ArraySort(comparefn) {
2    CHECK_OBJECT_COERCIBLE(this,"Array.prototype.sort");
3    var array = TO_OBJECT(this);
4    var length = TO_LENGTH(array.length);
5    return InnerArraySort(array, length, comparefn);
6}
7function InnerArraySort(array, length, comparefn) {
8// 比较函数未传入
9if (!IS_CALLABLE(comparefn)) {
10      comparefn = function (x, y) {
11        if (x === y) return 0;
12        if (%_IsSmi(x) && %_IsSmi(y)) {
13          return %SmiLexicographicCompare(x, y);
14        }
15        x = TO_STRING(x);
16        y = TO_STRING(y);
17        if (x == y) return 0;
18        else return x < y ? -1 : 1;
19   };
20}
21function InsertionSort(a, from, to) {
22  // 插入排序
23  for (var i = from + 1; i < to; i++) {
24        var element = a[i];
25        for (var j = i - 1; j >= from; j--) {
26          var tmp = a[j];
27          var order = comparefn(tmp, element);
28          if (order > 0) {
29            a[j + 1] = tmp;
30          } else {
31            break;
32          }
33        }
34      a[j + 1] = element;
35   }
36}
37function GetThirdIndex(a, from, to) {   // 元素个数大于1000时寻找哨兵元素
38  var t_array = new InternalArray();
39  var increment = 200 + ((to - from) & 15);
40  var j = 0;
41  from += 1;
42  to -= 1;
43  for (var i = from; i < to; i += increment) {
44     t_array[j] = [i, a[i]];
45     j++;
46  }
47  t_array.sort(function(a, b) {
48     return comparefn(a[1], b[1]);
49  });
50  var third_index = t_array[t_array.length >> 1][0];
51  return third_index;
52}
53function QuickSort(a, from, to) {  // 快速排序实现
54      //哨兵位置
55      var third_index = 0;
56      while (true) {
57        if (to - from <= 10) {
58          InsertionSort(a, from, to); // 数据量小，使用插入排序，速度较快
59          return;
60        }
61        if (to - from > 1000) {
62          third_index = GetThirdIndex(a, from, to);
63        } else {
64          // 小于1000 直接取中点
65          third_index = from + ((to - from) >> 1);
66        }
67        // 下面开始快排
68        var v0 = a[from];
69        var v1 = a[to - 1];
70        var v2 = a[third_index];
71        var c01 = comparefn(v0, v1);
72        if (c01 > 0) {
73          var tmp = v0;
74          v0 = v1;
75          v1 = tmp;
76        }
77        var c02 = comparefn(v0, v2);
78        if (c02 >= 0) {
79          var tmp = v0;
80          v0 = v2;
81          v2 = v1;
82          v1 = tmp;
83        } else {
84          var c12 = comparefn(v1, v2);
85          if (c12 > 0) {
86            var tmp = v1;
87            v1 = v2;
88            v2 = tmp;
89          }
90        }
91        a[from] = v0;
92        a[to - 1] = v2;
93        var pivot = v1;
94        var low_end = from + 1; 
95        var high_start = to - 1;
96        a[third_index] = a[low_end];
97        a[low_end] = pivot;
98        partition: for (var i = low_end + 1; i < high_start; i++) {
99          var element = a[i];
100          var order = comparefn(element, pivot);
101          if (order < 0) {
102            a[i] = a[low_end];
103            a[low_end] = element;
104            low_end++;
105          } else if (order > 0) {
106            do {
107              high_start--;
108              if (high_start == i) break partition;
109              var top_elem = a[high_start];
110              order = comparefn(top_elem, pivot);
111            } while (order > 0);
112            a[i] = a[high_start];
113            a[high_start] = element;
114            if (order < 0) {
115              element = a[i];
116              a[i] = a[low_end];
117              a[low_end] = element;
118              low_end++;
119            }
120          }
121        }
122        // 快排的核心思路，递归调用快速排序方法
123        if (to - high_start < low_end - from) {
124          QuickSort(a, high_start, to);
125          to = low_end;
126        } else {
127          QuickSort(a, from, low_end);
128          from = high_start;
129        }
130    }
131  }