问答题【840/1749】二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
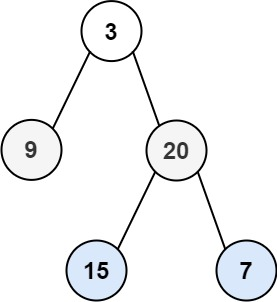
预览
输入: root = [3,9,20,null,null,15,7]
输出: [[3],[9,20],[15,7]]
示例 2:
输入: root = [1]
输出: [[1]]
示例 3:
输入: root = []
输出: []
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
1/** 2 * Definition for a binary tree node. 3 * function TreeNode(val, left, right) { 4 * this.val = (val===undefined ? 0 : val) 5 * this.left = (left===undefined ? null : left) 6 * this.right = (right===undefined ? null : right) 7 * } 8 */ 9/** 10 * @param {TreeNode} root 11 * @return {number[][]} 12 */ 13var levelOrder = function(root) { 14 15};
难度:
2022-05-16 创建参考答案
题目要点
个人笔记
参考答案:
方法1.广度优先遍历
- 思路:准备一个队列,将根节点加入队列,当队列不为空的时候循环队列,每次循环拿到当前队列的大小,在循环当前层的每个元素,然后加入输出数组ret中,如果这个元素存在左右节点则将左右节点加入队列
- 复杂度分析:时间复杂度
O(n),每个点进队出队各一次,故渐进时间复杂度为O(n)。空间复杂度O(n),队列中元素的个数不超过 n 个
1var levelOrder = function(root) { 2 const ret = []; 3 if (!root) { 4 return ret; 5 } 6 7 const q = []; 8 q.push(root);//初始队列 9 while (q.length !== 0) { 10 const currentLevelSize = q.length;//当前层节点的数量 11 ret.push([]);//新的层推入数组 12 for (let i = 1; i <= currentLevelSize; ++i) {//循环当前层的节点 13 const node = q.shift(); 14 ret[ret.length - 1].push(node.val);//推入当前层的数组 15 if (node.left) q.push(node.left);//检查左节点,存在左节点就继续加入队列 16 if (node.right) q.push(node.right);//检查左右节点,存在右节点就继续加入队列 17 } 18 } 19 20 return ret; 21}; 22
方法2:深度优先遍历
- 思路:从根节点开始不断递归左右子树,透传step层数和res输出数组。
- 复杂度分析:时间复杂度
O(n),n是节点的个数。空间复杂度O(n),n是树的高度。
1var levelOrder = function(root) { 2 if(!root) return [] 3 let res = [] 4 dfs(root, 0, res) 5 return res 6}; 7 8function dfs(root, step, res){//每层透传当前节点,层数,和输出数组 9 if(root){ 10 if(!res[step]) res[step] = []//初始化当前层数组 11 res[step].push(root.val)//当前节点加入当前层数组 12 dfs(root.left, step + 1, res)//step+1,递归左节点 13 dfs(root.right, step + 1, res)//step+1,递归右节点 14 } 15}
最近更新时间:2022-05-16
赞赏支持

题库维护不易,您的支持就是我们最大的动力!
